大学入学共通テスト（数学） 過去問
令和6年度（2024年度）追・試験
問82 (数学Ⅱ・数学B（第2問） 問11)
問題文
f（x）＝x3−3x2＋6とする。
（4）g（x）＝x3−6x2＋6x＋2とし、座標平面において2点（t，f（t））、（t，g（t））を結んでできる線分をl2とおく。また、rを実数とし、実数tが
r≦t≦r＋1の範囲を動くとき、l2が通過する部分の面積をSとする。
（ⅰ）f（x）−g（x）の値は、（ ナ ）。したがって、すべての実数rに対して、S＝（ ニ ）が成り立つ。
（ ニ ）にあてはまるものを1つ選べ。
（4）g（x）＝x3−6x2＋6x＋2とし、座標平面において2点（t，f（t））、（t，g（t））を結んでできる線分をl2とおく。また、rを実数とし、実数tが
r≦t≦r＋1の範囲を動くとき、l2が通過する部分の面積をSとする。
（ⅰ）f（x）−g（x）の値は、（ ナ ）。したがって、すべての実数rに対して、S＝（ ニ ）が成り立つ。
（ ニ ）にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和6年度（2024年度）追・試験 問82（数学Ⅱ・数学B（第2問） 問11） （訂正依頼・報告はこちら）
f（x）＝x3−3x2＋6とする。
（4）g（x）＝x3−6x2＋6x＋2とし、座標平面において2点（t，f（t））、（t，g（t））を結んでできる線分をl2とおく。また、rを実数とし、実数tが
r≦t≦r＋1の範囲を動くとき、l2が通過する部分の面積をSとする。
（ⅰ）f（x）−g（x）の値は、（ ナ ）。したがって、すべての実数rに対して、S＝（ ニ ）が成り立つ。
（ ニ ）にあてはまるものを1つ選べ。
（4）g（x）＝x3−6x2＋6x＋2とし、座標平面において2点（t，f（t））、（t，g（t））を結んでできる線分をl2とおく。また、rを実数とし、実数tが
r≦t≦r＋1の範囲を動くとき、l2が通過する部分の面積をSとする。
（ⅰ）f（x）−g（x）の値は、（ ナ ）。したがって、すべての実数rに対して、S＝（ ニ ）が成り立つ。
（ ニ ）にあてはまるものを1つ選べ。
正解！素晴らしいです
残念...
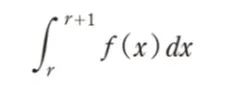
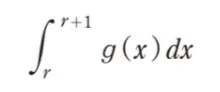
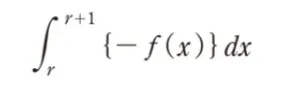
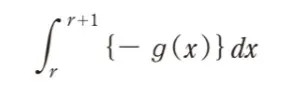
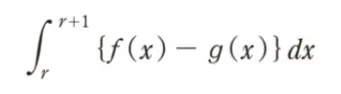
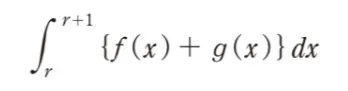
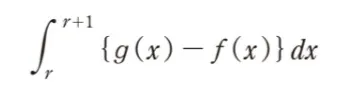
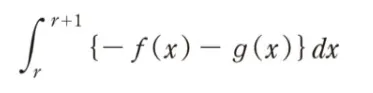
この過去問の解説 （1件）
01
f（x）-g（x）=3x2-6x+4
この判別式は、62-4・3・4＜0
なので常に正であることが分かります。
f（x）-g（x）＞0より、常にf（x）＞g（x）が成り立つことから
が常に成り立ちます。
正解です。
積分の特性を復習しておくことが大切です。
参考になった数0
この解説の修正を提案する
前の問題（問81）へ
令和6年度（2024年度）追・試験 問題一覧
次の問題（問83）へ