大学入学共通テスト（数学） 過去問
令和7年度（2025年度）本試験
問17 (数学Ⅰ・数学A（第2問） 問3)
問題文
〔1〕花子さんと太郎さんは、公園にある二つの小さな噴水と一つの大きな噴水の高さについて話している。
花子：あの中央の大きな噴水の高さは何メートルだろう。
太郎：実際に高さを測定するのは難しそうだね。噴水の水がえがく曲線は、放物線になると聞いたことがあるよ。
花子：じゃあ、放物線と仮定して、およその高さを考えてみよう。
花子さんと太郎さんは、噴水の高さについて次のように考えることにした。噴水の水がえがく曲線は三つとも放物線とする。三つの噴水の水が出る位置は水平な地面にある。図1のように座標軸が定められた平面上に、三つの噴水を正面から見た図をかく。左右の小さな噴水の水がえがく放物線については後の仮定1を、中央の大きな噴水の水がえがく放物線については後の仮定2を設定する。図1のP1，P2，P3は噴水の水が出る位置である。なお、長さの単位はメートルであるが、以下では省略する。
仮定1
●左側の小さな噴水の水がえがく放物線C1は、x軸上の点P1｛−（5／2），0｝から出て点｛（1／2），0｝に至る。
●右側の小さな噴水の水がえがく放物線C3は、x軸上の点P3｛（5／2），0｝から出て点｛−（1／2），0｝に至る。
●C1とC3はともに点（0，1）を通る。
仮定2
中央の大きな噴水の水がえがく放物線C2は、x軸上の点P2｛（3／2），0｝から出てC3の頂点とC1の頂点を通る。
（1）仮定1と仮定2のもとで考える。
C1をグラフにもつ2次関数を
y＝ax2＋bx＋cとする。
このときc＝（ ア ）であり、また
y＝−（［ イ ］／［ ウ ］）x2−（［ エ ］／［ オ ］）x＋（ ア ）
である。
C1の頂点のy座標は（ カ ）／（ キ ）である。
このことを用いると、C2の頂点のy座標は（ クケ ）／（ コサ ）であることがわかる。
したがって、大きな噴水の高さは、小さな噴水の高さの（ シ ）である。
（ カ ）、（ キ ）にあてはまるものを1つ選べ。
花子：あの中央の大きな噴水の高さは何メートルだろう。
太郎：実際に高さを測定するのは難しそうだね。噴水の水がえがく曲線は、放物線になると聞いたことがあるよ。
花子：じゃあ、放物線と仮定して、およその高さを考えてみよう。
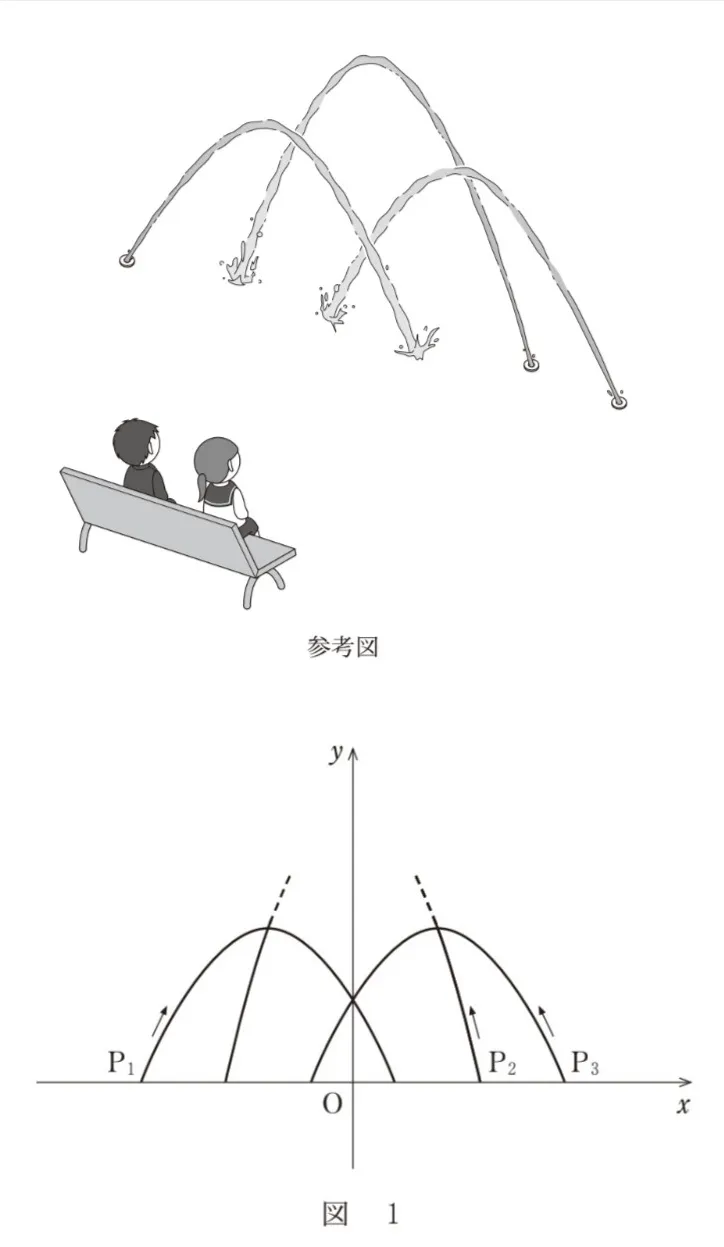
花子さんと太郎さんは、噴水の高さについて次のように考えることにした。噴水の水がえがく曲線は三つとも放物線とする。三つの噴水の水が出る位置は水平な地面にある。図1のように座標軸が定められた平面上に、三つの噴水を正面から見た図をかく。左右の小さな噴水の水がえがく放物線については後の仮定1を、中央の大きな噴水の水がえがく放物線については後の仮定2を設定する。図1のP1，P2，P3は噴水の水が出る位置である。なお、長さの単位はメートルであるが、以下では省略する。
仮定1
●左側の小さな噴水の水がえがく放物線C1は、x軸上の点P1｛−（5／2），0｝から出て点｛（1／2），0｝に至る。
●右側の小さな噴水の水がえがく放物線C3は、x軸上の点P3｛（5／2），0｝から出て点｛−（1／2），0｝に至る。
●C1とC3はともに点（0，1）を通る。
仮定2
中央の大きな噴水の水がえがく放物線C2は、x軸上の点P2｛（3／2），0｝から出てC3の頂点とC1の頂点を通る。
（1）仮定1と仮定2のもとで考える。
C1をグラフにもつ2次関数を
y＝ax2＋bx＋cとする。
このときc＝（ ア ）であり、また
y＝−（［ イ ］／［ ウ ］）x2−（［ エ ］／［ オ ］）x＋（ ア ）
である。
C1の頂点のy座標は（ カ ）／（ キ ）である。
このことを用いると、C2の頂点のy座標は（ クケ ）／（ コサ ）であることがわかる。
したがって、大きな噴水の高さは、小さな噴水の高さの（ シ ）である。
（ カ ）、（ キ ）にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和7年度（2025年度）本試験 問17（数学Ⅰ・数学A（第2問） 問3） （訂正依頼・報告はこちら）
〔1〕花子さんと太郎さんは、公園にある二つの小さな噴水と一つの大きな噴水の高さについて話している。
花子：あの中央の大きな噴水の高さは何メートルだろう。
太郎：実際に高さを測定するのは難しそうだね。噴水の水がえがく曲線は、放物線になると聞いたことがあるよ。
花子：じゃあ、放物線と仮定して、およその高さを考えてみよう。
花子さんと太郎さんは、噴水の高さについて次のように考えることにした。噴水の水がえがく曲線は三つとも放物線とする。三つの噴水の水が出る位置は水平な地面にある。図1のように座標軸が定められた平面上に、三つの噴水を正面から見た図をかく。左右の小さな噴水の水がえがく放物線については後の仮定1を、中央の大きな噴水の水がえがく放物線については後の仮定2を設定する。図1のP1，P2，P3は噴水の水が出る位置である。なお、長さの単位はメートルであるが、以下では省略する。
仮定1
●左側の小さな噴水の水がえがく放物線C1は、x軸上の点P1｛−（5／2），0｝から出て点｛（1／2），0｝に至る。
●右側の小さな噴水の水がえがく放物線C3は、x軸上の点P3｛（5／2），0｝から出て点｛−（1／2），0｝に至る。
●C1とC3はともに点（0，1）を通る。
仮定2
中央の大きな噴水の水がえがく放物線C2は、x軸上の点P2｛（3／2），0｝から出てC3の頂点とC1の頂点を通る。
（1）仮定1と仮定2のもとで考える。
C1をグラフにもつ2次関数を
y＝ax2＋bx＋cとする。
このときc＝（ ア ）であり、また
y＝−（［ イ ］／［ ウ ］）x2−（［ エ ］／［ オ ］）x＋（ ア ）
である。
C1の頂点のy座標は（ カ ）／（ キ ）である。
このことを用いると、C2の頂点のy座標は（ クケ ）／（ コサ ）であることがわかる。
したがって、大きな噴水の高さは、小さな噴水の高さの（ シ ）である。
（ カ ）、（ キ ）にあてはまるものを1つ選べ。
花子：あの中央の大きな噴水の高さは何メートルだろう。
太郎：実際に高さを測定するのは難しそうだね。噴水の水がえがく曲線は、放物線になると聞いたことがあるよ。
花子：じゃあ、放物線と仮定して、およその高さを考えてみよう。
花子さんと太郎さんは、噴水の高さについて次のように考えることにした。噴水の水がえがく曲線は三つとも放物線とする。三つの噴水の水が出る位置は水平な地面にある。図1のように座標軸が定められた平面上に、三つの噴水を正面から見た図をかく。左右の小さな噴水の水がえがく放物線については後の仮定1を、中央の大きな噴水の水がえがく放物線については後の仮定2を設定する。図1のP1，P2，P3は噴水の水が出る位置である。なお、長さの単位はメートルであるが、以下では省略する。
仮定1
●左側の小さな噴水の水がえがく放物線C1は、x軸上の点P1｛−（5／2），0｝から出て点｛（1／2），0｝に至る。
●右側の小さな噴水の水がえがく放物線C3は、x軸上の点P3｛（5／2），0｝から出て点｛−（1／2），0｝に至る。
●C1とC3はともに点（0，1）を通る。
仮定2
中央の大きな噴水の水がえがく放物線C2は、x軸上の点P2｛（3／2），0｝から出てC3の頂点とC1の頂点を通る。
（1）仮定1と仮定2のもとで考える。
C1をグラフにもつ2次関数を
y＝ax2＋bx＋cとする。
このときc＝（ ア ）であり、また
y＝−（［ イ ］／［ ウ ］）x2−（［ エ ］／［ オ ］）x＋（ ア ）
である。
C1の頂点のy座標は（ カ ）／（ キ ）である。
このことを用いると、C2の頂点のy座標は（ クケ ）／（ コサ ）であることがわかる。
したがって、大きな噴水の高さは、小さな噴水の高さの（ シ ）である。
（ カ ）、（ キ ）にあてはまるものを1つ選べ。
- カ：1 キ：7
- カ：3 キ：5
- カ：4 キ：5
- カ：7 キ：6
- カ：9 キ：5
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
この問題は、これまでの問題で求めたa,b,cからできる2次関数の式を平方完成する問題です。
まず、これまでの問題より、a=ー(4/5),b=ー(8/5),c=1なので、
2次関数の式は、
y=ー(4/5)x2ー(8/5)x+1となり、これを平方完成していきます。
①まず、x2の係数をくくり出します。
y=ー(4/5)(x2ー2x)+1
②次に、(x2ー2x)の部分を(xー〇)2ー〇の形になるよう変形します。
y=ー(4/5){(xー1)2ー1}+1
※(x2ーpx)={xー(p/2)}2ー(2/p)2
③(xー1)2はそのままで、{}部分を展開して、整理します。
y=ー(4/5)(xー1)2+(9/5)
これより、カ：9 キ：5となります。
参考になった数0
この解説の修正を提案する
前の問題（問16）へ
令和7年度（2025年度）本試験 問題一覧
次の問題（問18）へ