大学入学共通テスト(数学) 過去問
令和7年度(2025年度)本試験
問80 (数学Ⅱ・数学B(第4問) 問2)
問題文
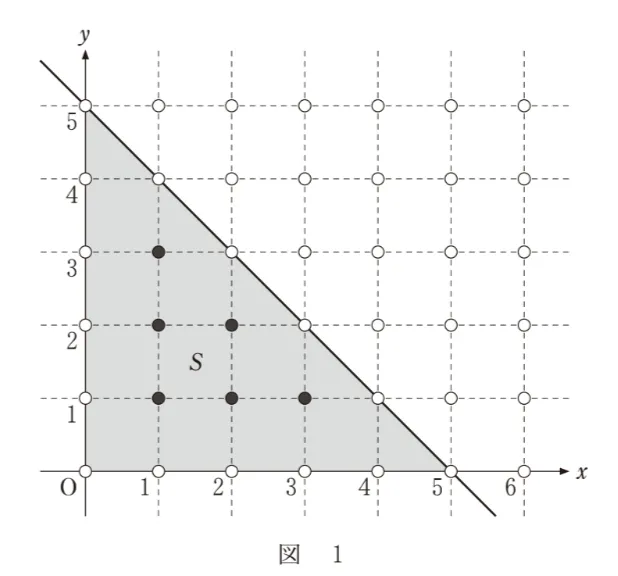
例えば、直線y=−x+5とx軸、y軸で囲まれた図形をSとする。Sは図1の灰色部分であり、Sの内部にある格子点を黒丸、内部にない格子点を白丸で表している。したがって、Sの内部にある格子点の個数は6である。
(1)直線y=3xとx軸、直線x=21で囲まれた図形をTとする。Tの内部にある格子点の個数を考える。
直線x=1上の格子点でTの内部にあるものは、点(1,1)と点(1,2)の2個である。点(1,0)と点(1,3)はTの境界にあるため、内部にはない。
nを整数とする。直線x=nがTの内部にある格子点を通るのは、1≦n≦20のときである。1≦n≦20のとき、直線x=n上の格子点でTの内部にあるものの個数をanとおく。a1=2であり、a2=( ア )、a3=( イ )である。数列{an}は( ウ )が( エ )の( オ )数列である。
したがって、Tの内部にある格子点の個数は( カキク )である。
( ウ )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和7年度(2025年度)本試験 問80(数学Ⅱ・数学B(第4問) 問2) (訂正依頼・報告はこちら)
例えば、直線y=−x+5とx軸、y軸で囲まれた図形をSとする。Sは図1の灰色部分であり、Sの内部にある格子点を黒丸、内部にない格子点を白丸で表している。したがって、Sの内部にある格子点の個数は6である。
(1)直線y=3xとx軸、直線x=21で囲まれた図形をTとする。Tの内部にある格子点の個数を考える。
直線x=1上の格子点でTの内部にあるものは、点(1,1)と点(1,2)の2個である。点(1,0)と点(1,3)はTの境界にあるため、内部にはない。
nを整数とする。直線x=nがTの内部にある格子点を通るのは、1≦n≦20のときである。1≦n≦20のとき、直線x=n上の格子点でTの内部にあるものの個数をanとおく。a1=2であり、a2=( ア )、a3=( イ )である。数列{an}は( ウ )が( エ )の( オ )数列である。
したがって、Tの内部にある格子点の個数は( カキク )である。
( ウ )にあてはまるものを1つ選べ。

- 公差
- 公比
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問79)へ
令和7年度(2025年度)本試験 問題一覧
次の問題(問81)へ