大学入学共通テスト(数学) 過去問
令和7年度(2025年度)本試験
問84 (数学Ⅱ・数学B(第4問) 問6)
問題文
座標平面上で、x座標とy座標がともに整数である点を格子点という。いくつかの直線や曲線で囲まれた図形の内部にある格子点の個数を考えよう。ただし、図形の内部は、境界(境界線)を含まないものとする。
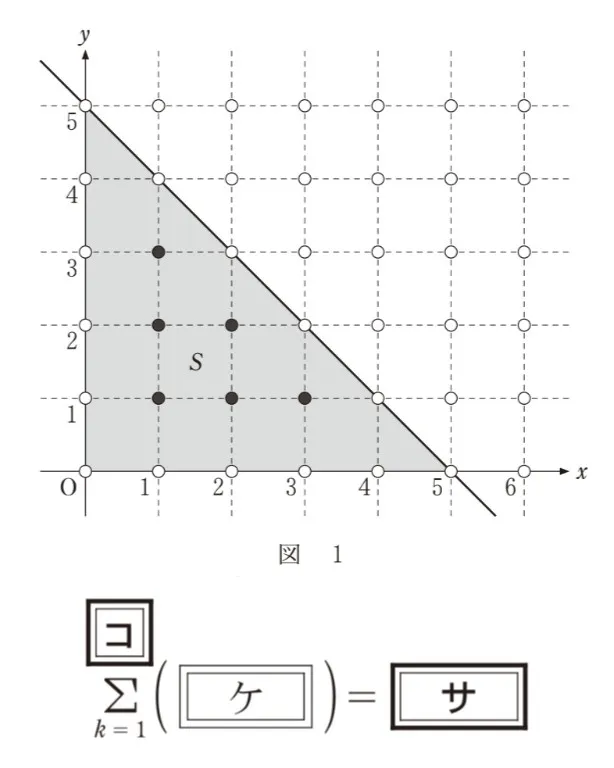
例えば、直線y=−x+5とx軸、y軸で囲まれた図形をSとする。Sは図1の灰色部分であり、Sの内部にある格子点を黒丸、内部にない格子点を白丸で表している。したがって、Sの内部にある格子点の個数は6である。
(2)nを自然数とする。
関数y=2xのグラフとx軸、y軸および直線x=n+1で囲まれた図形をUとする。
kを整数とする。直線x=kがUの内部にある格子点を通るとき、直線x=k上の格子点でUの内部にあるものの個数は( ケ )である。したがって、Uの内部にある格子点の個数は以下の式となる。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和7年度(2025年度)本試験 問84(数学Ⅱ・数学B(第4問) 問6) (訂正依頼・報告はこちら)
座標平面上で、x座標とy座標がともに整数である点を格子点という。いくつかの直線や曲線で囲まれた図形の内部にある格子点の個数を考えよう。ただし、図形の内部は、境界(境界線)を含まないものとする。
例えば、直線y=−x+5とx軸、y軸で囲まれた図形をSとする。Sは図1の灰色部分であり、Sの内部にある格子点を黒丸、内部にない格子点を白丸で表している。したがって、Sの内部にある格子点の個数は6である。
(2)nを自然数とする。
関数y=2xのグラフとx軸、y軸および直線x=n+1で囲まれた図形をUとする。
kを整数とする。直線x=kがUの内部にある格子点を通るとき、直線x=k上の格子点でUの内部にあるものの個数は( ケ )である。したがって、Uの内部にある格子点の個数は以下の式となる。

- n−1
- n
- n+1
- 2n−1
- 2n
- 2n+1
- 2n−1
- 2n
- 2n+1
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問83)へ
令和7年度(2025年度)本試験 問題一覧
次の問題(問85)へ