大学入学共通テスト（数学） 過去問
令和7年度（2025年度）本試験
問103 (数学Ⅱ・数学B（第6問） 問7)
問題文
画像内の空欄（ シ ）にあてはまるものを1つ選べ。
Oを原点とする座標空間において、Oを中心とする半径1の球面をSとする。S上に二つの点A（1，0，0）、B（a，√（1−a2），0）をとる。ただし、aは−1＜a＜1を満たす実数とする。S上の点Cを、ΔABCが正三角形となるようにとれるかどうかを考えてみよう。
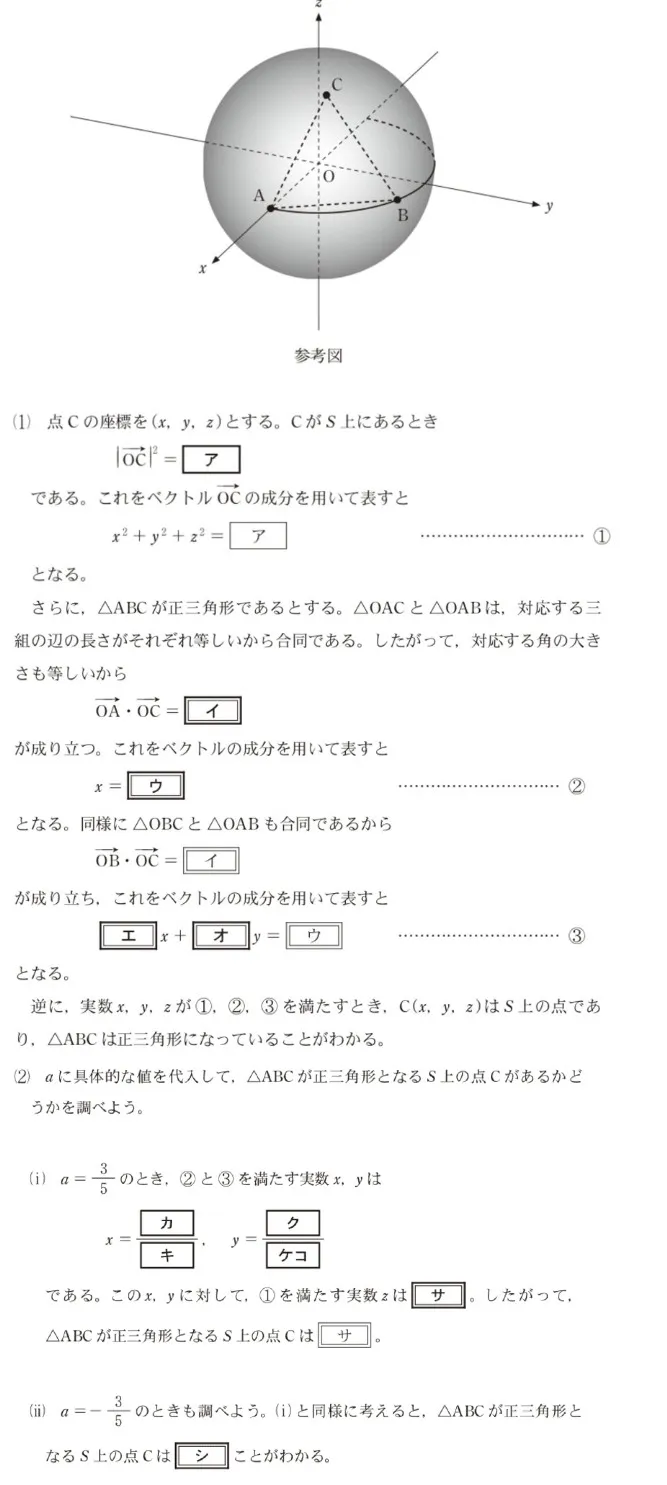
Oを原点とする座標空間において、Oを中心とする半径1の球面をSとする。S上に二つの点A（1，0，0）、B（a，√（1−a2），0）をとる。ただし、aは−1＜a＜1を満たす実数とする。S上の点Cを、ΔABCが正三角形となるようにとれるかどうかを考えてみよう。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和7年度（2025年度）本試験 問103（数学Ⅱ・数学B（第6問） 問7） （訂正依頼・報告はこちら）
画像内の空欄（ シ ）にあてはまるものを1つ選べ。
Oを原点とする座標空間において、Oを中心とする半径1の球面をSとする。S上に二つの点A（1，0，0）、B（a，√（1−a2），0）をとる。ただし、aは−1＜a＜1を満たす実数とする。S上の点Cを、ΔABCが正三角形となるようにとれるかどうかを考えてみよう。
Oを原点とする座標空間において、Oを中心とする半径1の球面をSとする。S上に二つの点A（1，0，0）、B（a，√（1−a2），0）をとる。ただし、aは−1＜a＜1を満たす実数とする。S上の点Cを、ΔABCが正三角形となるようにとれるかどうかを考えてみよう。
- ない
- ちょうど一つある
- ちょうど二つある
- ちょうど三つある
- ちょうど四つある
- 無限に多くある
正解！素晴らしいです
残念...
この過去問の解説
前の問題（問102）へ
令和7年度（2025年度）本試験 問題一覧
次の問題（問104）へ