大学入学共通テスト（数学） 過去問
令和7年度（2025年度）追・試験
問2 (数学Ⅰ・数学A（第1問） 問2)
問題文
以下（ エ ），（ オ ），（ カ ）にあてはまるものを一つ選べ。
〔1〕分数を小数で表すときの仕組みについて考えよう。
例えば2／13は、計算例1のような割り算を行うと小数で表すことができる。この場合、1回目の割り算の余りは7で、2回目の割り算の余りは5である。
2／13以外の分数の場合も同様に、1回目の割り算の余り、2回目の割り算の余り、3回目の割り算の余り、・・・ということにする。
（2）m＜nである自然数m、nに対し、m／nを計算例のようにして小数で表すことを考える。mをnで割ったときの各回の割り算の余りに着目すると、余りに0が出てくる場合は、m／nは（ エ ）となる。余りに0が出てこない場合は（ オ ）から、m／nは（ カ ）となる。
〔1〕分数を小数で表すときの仕組みについて考えよう。
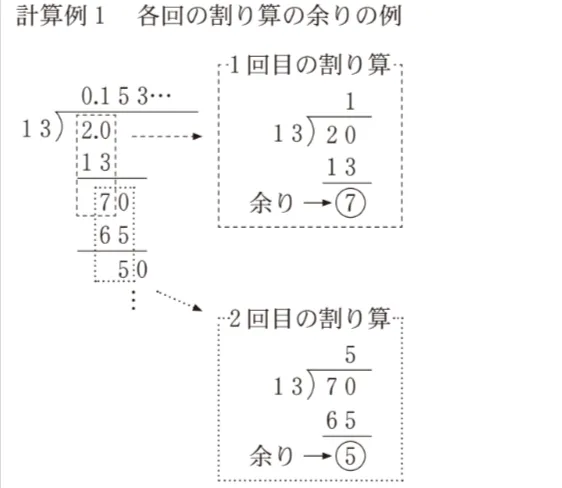
例えば2／13は、計算例1のような割り算を行うと小数で表すことができる。この場合、1回目の割り算の余りは7で、2回目の割り算の余りは5である。
2／13以外の分数の場合も同様に、1回目の割り算の余り、2回目の割り算の余り、3回目の割り算の余り、・・・ということにする。
（2）m＜nである自然数m、nに対し、m／nを計算例のようにして小数で表すことを考える。mをnで割ったときの各回の割り算の余りに着目すると、余りに0が出てくる場合は、m／nは（ エ ）となる。余りに0が出てこない場合は（ オ ）から、m／nは（ カ ）となる。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和7年度（2025年度）追・試験 問2（数学Ⅰ・数学A（第1問） 問2） （訂正依頼・報告はこちら）
以下（ エ ），（ オ ），（ カ ）にあてはまるものを一つ選べ。
〔1〕分数を小数で表すときの仕組みについて考えよう。
例えば2／13は、計算例1のような割り算を行うと小数で表すことができる。この場合、1回目の割り算の余りは7で、2回目の割り算の余りは5である。
2／13以外の分数の場合も同様に、1回目の割り算の余り、2回目の割り算の余り、3回目の割り算の余り、・・・ということにする。
（2）m＜nである自然数m、nに対し、m／nを計算例のようにして小数で表すことを考える。mをnで割ったときの各回の割り算の余りに着目すると、余りに0が出てくる場合は、m／nは（ エ ）となる。余りに0が出てこない場合は（ オ ）から、m／nは（ カ ）となる。
〔1〕分数を小数で表すときの仕組みについて考えよう。
例えば2／13は、計算例1のような割り算を行うと小数で表すことができる。この場合、1回目の割り算の余りは7で、2回目の割り算の余りは5である。
2／13以外の分数の場合も同様に、1回目の割り算の余り、2回目の割り算の余り、3回目の割り算の余り、・・・ということにする。
（2）m＜nである自然数m、nに対し、m／nを計算例のようにして小数で表すことを考える。mをnで割ったときの各回の割り算の余りに着目すると、余りに0が出てくる場合は、m／nは（ エ ）となる。余りに0が出てこない場合は（ オ ）から、m／nは（ カ ）となる。
- エ：整数 オ：割り算を続けても同じ余りが出てくることはない カ：循環小数
- エ：有限小数 オ：割り算を続けても同じ余りが出てくることはない カ：循環しない無限小数
- エ：循環小数 オ：割り算を続けても同じ余りが出てくることはない カ：整数
- エ：循環しない無限小数 オ：割り算を続けても同じ余りが出てくることはない カ：有限小数
- エ：整数 オ：割り算を続けても同じ余りが出てくることはない カ：整数
- エ：有限小数 オ：割り算を続けると必ず同じ余りが出てくる カ：循環しない無限小数
- エ：循環小数 オ：割り算を続けると必ず同じ余りが出てくる カ：有限小数
- エ：循環しない無限小数 オ：割り算を続けると必ず同じ余りが出てくる カ：有限小数
- エ：整数 オ：割り算を続けると必ず同じ余りが出てくる カ：循環小数
- エ：有限小数 オ：割り算を続けると必ず同じ余りが出てくる カ：循環小数
正解！素晴らしいです
残念...
この過去問の解説
前の問題（問1）へ
令和7年度（2025年度）追・試験 問題一覧
次の問題（問3）へ