大学入学共通テスト(数学) 過去問
令和7年度(2025年度)追・試験
問16 (数学Ⅰ・数学A(第2問) 問5)
問題文
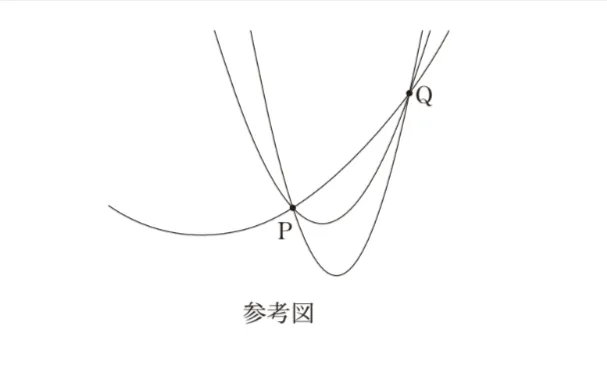
(2)花子さんと太郎さんは、a=2、b=−7、c=7と定めたとき、関数y=2x2−7x+7のグラフが、点P(1,2)と点Q(3,4)を通ることに気づいて、コンピュータの画面を見ながら、次のように話している。
花子:このグラフは点P(1,2),Q(3,4)を通っているね。
太郎:aの値を変えるとグラフはどうなるのかな。
花子:aの値だけを変えたら、P,Qを通らなくなったよ。P,Qを通るようにするには、aの値に応じてbとcの値をどう変えたらよいのかな。
0でない実数aに対して
b=( オ )―( カ )a
c=( キ )+( ク )a
とすれば、関数
y=ax2+([ オ ]―[ カ ]a)x+( キ )+( ク )a・・・①
のグラフは2点PとQを通る。
(4)次に、花子さんと太郎さんはaの値を0より小さい範囲で変えながら、関数①のグラフを表示させている。このとき、次の(A),(B),(C)のうちで、起こり得るものは( シ )。
(A) 関数のグラフが点(0,3)を通る。
(B) 関数のグラフとx軸の負の部分が交わる。
(C) 関数のグラフの頂点のx座標が2以下である。
( シ )にあてはまるものを一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和7年度(2025年度)追・試験 問16(数学Ⅰ・数学A(第2問) 問5) (訂正依頼・報告はこちら)
(2)花子さんと太郎さんは、a=2、b=−7、c=7と定めたとき、関数y=2x2−7x+7のグラフが、点P(1,2)と点Q(3,4)を通ることに気づいて、コンピュータの画面を見ながら、次のように話している。
花子:このグラフは点P(1,2),Q(3,4)を通っているね。
太郎:aの値を変えるとグラフはどうなるのかな。
花子:aの値だけを変えたら、P,Qを通らなくなったよ。P,Qを通るようにするには、aの値に応じてbとcの値をどう変えたらよいのかな。
0でない実数aに対して
b=( オ )―( カ )a
c=( キ )+( ク )a
とすれば、関数
y=ax2+([ オ ]―[ カ ]a)x+( キ )+( ク )a・・・①
のグラフは2点PとQを通る。
(4)次に、花子さんと太郎さんはaの値を0より小さい範囲で変えながら、関数①のグラフを表示させている。このとき、次の(A),(B),(C)のうちで、起こり得るものは( シ )。
(A) 関数のグラフが点(0,3)を通る。
(B) 関数のグラフとx軸の負の部分が交わる。
(C) 関数のグラフの頂点のx座標が2以下である。
( シ )にあてはまるものを一つ選べ。

- ない
- (A)だけである
- (B)だけである
- (C)だけである
- (A)と(B)だけである
- (A)と(C)だけである
- (B)と(C)だけである
- (A)と(B)と(C)のすべてである
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問15)へ
令和7年度(2025年度)追・試験 問題一覧
次の問題(問17)へ