大学入学共通テスト(数学) 過去問
令和7年度(2025年度)追・試験
問49 (数学Ⅱ・数学B(第2問) 問5)
問題文
実数sは−2<s<2を満たし、実数tはt>0を満たすとする。Oを原点とする座標平面において、方程式
x2+y2=4
が表す円をC0,方程式
x2−2sx+y2−2ty+s2=0・・・・・①
が表す円をCとする。
(2)CとC0が接する場合を考える。CとC0が接したまま実数sが−2<s<2の範囲を動くとき、Cの中心が描く図形について考えよう。
(ⅱ)Cの中心が描く図形の概形を実線で表したものは( ク )である。
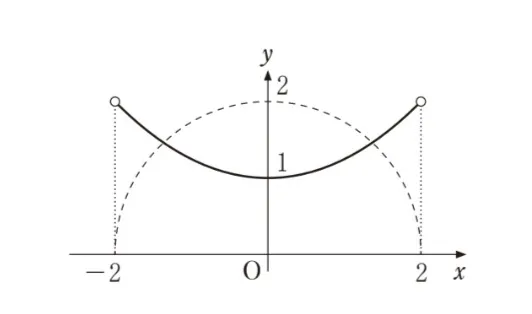
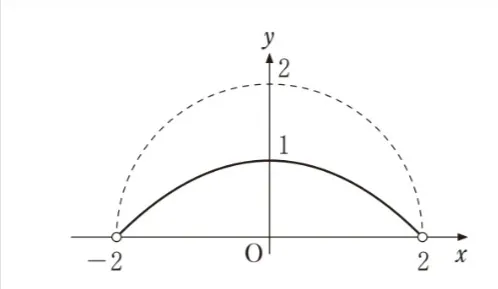
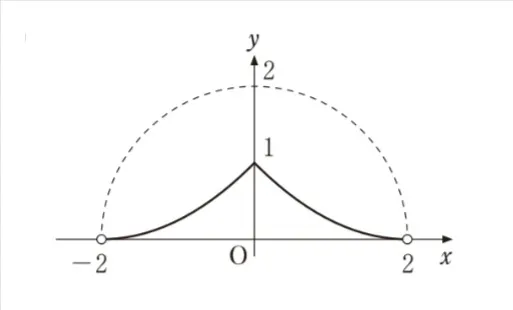
( ク )については、最も適当なものを、次の選択肢のうちから一つ選べ。ただし、選択肢ではC0のy>0の部分をそれぞれ破線で表している。

このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和7年度(2025年度)追・試験 問49(数学Ⅱ・数学B(第2問) 問5) (訂正依頼・報告はこちら)
実数sは−2<s<2を満たし、実数tはt>0を満たすとする。Oを原点とする座標平面において、方程式
x2+y2=4
が表す円をC0,方程式
x2−2sx+y2−2ty+s2=0・・・・・①
が表す円をCとする。
(2)CとC0が接する場合を考える。CとC0が接したまま実数sが−2<s<2の範囲を動くとき、Cの中心が描く図形について考えよう。
(ⅱ)Cの中心が描く図形の概形を実線で表したものは( ク )である。
( ク )については、最も適当なものを、次の選択肢のうちから一つ選べ。ただし、選択肢ではC0のy>0の部分をそれぞれ破線で表している。

正解!素晴らしいです
残念...




この過去問の解説 (1件)
01
解答:上に凸の放物線の図
解説:
(キ)の解答より、円Cの中心(s,t)の関係式は、以下のようになります。
t=-1/4s2+1
これは、tがsに関する2次関数であることを示しています。
また、s2の係数が負であることから、上に凸の関数を表しています。
したがって、上に凸の放物線が解答です。
上に凸の放物線を示している、この選択肢が解答です。
参考になった数0
この解説の修正を提案する
前の問題(問48)へ
令和7年度(2025年度)追・試験 問題一覧
次の問題(問50)へ