共通テスト（数学） 過去問
令和7年度（2025年度）追・試験
問74 (数学Ⅱ・数学B（第5問） 問6)
問題文
問題を解答するにあたっては、必要に応じて 正規分布表 を用いてもよい。
次のように設定されているくじを考える。くじを1回引いて得られる点を得点と呼ぶ。
くじの設定
中身の見えない箱の中に
000，001，002，・・・，998，999
の番号が、それぞれ一つずつ書かれたカードが1枚ずつ合計1000枚入っている。この箱の中から無作為に1枚のカードを取り出して番号を確認し、そのカードを箱の中に戻す試行を繰り返し行う。このとき、取り出したカードに書かれた番号によって、以下に示される点が得られるものとする。
●番号が「777」ならば、2000点
●番号の下二桁が「22」ならば、800点
●番号の下一桁が「1」ならば、100点
●上記以外ならば、0点
（2）くじの参加者にはあらかじめ十分な持ち点が与えられている。くじを1回引くたびに25点を引かれるとする。1回のくじ引きに対して、得点から25点を引いた差を損得点と呼ぶ。
（ⅰ）損得点を確率変数Yで表す。Yは、前問 の確率変数Xを用いて
Y＝X−（ キク ）
と表せる。（ キク ）＝cとおくと、Yのとり得る値はy1＝x1−c，
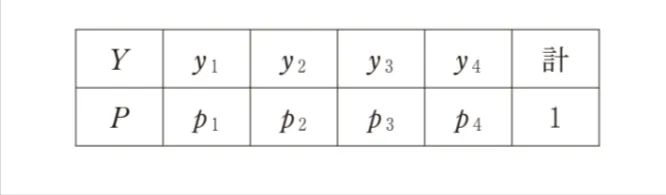
y2＝x2−c，y3＝x3−c，y4＝x4−cである。Yの確率分布は、（1）のp1，p2，p3，p4を用いて画像の表で与えられる。
確率変数Yの平均（期待値）E（Y）は、（1）のE（X）を用いて
E（Y）＝（ ケ ）
となる。また、確率変数Yの分散V（Y）は、（1）のV（X）を用いて
V（Y）＝（ コ ）
となる。
（ コ ）にあてはまるものを一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
共通テスト（数学）試験 令和7年度（2025年度）追・試験 問74（数学Ⅱ・数学B（第5問） 問6） （訂正依頼・報告はこちら）
問題を解答するにあたっては、必要に応じて 正規分布表 を用いてもよい。
次のように設定されているくじを考える。くじを1回引いて得られる点を得点と呼ぶ。
くじの設定
中身の見えない箱の中に
000，001，002，・・・，998，999
の番号が、それぞれ一つずつ書かれたカードが1枚ずつ合計1000枚入っている。この箱の中から無作為に1枚のカードを取り出して番号を確認し、そのカードを箱の中に戻す試行を繰り返し行う。このとき、取り出したカードに書かれた番号によって、以下に示される点が得られるものとする。
●番号が「777」ならば、2000点
●番号の下二桁が「22」ならば、800点
●番号の下一桁が「1」ならば、100点
●上記以外ならば、0点
（2）くじの参加者にはあらかじめ十分な持ち点が与えられている。くじを1回引くたびに25点を引かれるとする。1回のくじ引きに対して、得点から25点を引いた差を損得点と呼ぶ。
（ⅰ）損得点を確率変数Yで表す。Yは、前問 の確率変数Xを用いて
Y＝X−（ キク ）
と表せる。（ キク ）＝cとおくと、Yのとり得る値はy1＝x1−c，
y2＝x2−c，y3＝x3−c，y4＝x4−cである。Yの確率分布は、（1）のp1，p2，p3，p4を用いて画像の表で与えられる。
確率変数Yの平均（期待値）E（Y）は、（1）のE（X）を用いて
E（Y）＝（ ケ ）
となる。また、確率変数Yの分散V（Y）は、（1）のV（X）を用いて
V（Y）＝（ コ ）
となる。
（ コ ）にあてはまるものを一つ選べ。
- V（X）
- V（X）−c
- V（X）＋c
- cE（X）
- E（X）／c
正解！素晴らしいです
残念...
この過去問の解説 （3件）
01
同様にして
一般に V(aX+b)=a2V(X) が成り立つので
V(Y)=V(X-c)=V(X) と変換できます
確率変数をXからY=aX+bと1次式の形に変換した確率変数はよく出るので、以下の公式を覚えましょう
平均(期待値) E(aX+b)=aE(X)+b
分散 V(aX+b)=a2V(X)
標準偏差 σ(aX+b)=|a|σ(X)
なお、分散・標準偏差については平均とのずれ具合を示す値なので、定数項bの差分は影響ありません。
参考になった数0
この解説の修正を提案する
02
分散は数値データのばらつき具合を表すための指標ですので、
今回は確率に関係なく、全体的に得点cだけ一律に得点が下がるので、分散には影響を及ばしません。
そのため、V(Y)=V(X) となります。
詳細に求めますと、
yi-E(Y)=(xi-c)-(E(X)-c)=xi-E(X)
より、確率変数Xの分散V（X）は
V(Y)=(y1-E(Y))2p1+(y2-E(Y))2p2+(y3-E(Y))2p3+(y4-E(Y))2p4
=(x1-E(X))2p1+(x2-E(X))2p2+(x3-E(X))2p3+(x4-E(X))2p4
=V(X)
詳細に求めることも可能ですが、そもそも分散がどういった内容を表しているのかを理解していると回答が早くなります。
参考になった数0
この解説の修正を提案する
03
解答：V（X）
解説：
Xの分散は以下のようになります。
V（X）=（x1-E（X））2p1+（x2-E（X））2p2+（x3-E（X））2p3+（x4-E（X））2p4
Yの分散は以下のようになり、これを変形して示します。
V（Y）=（y1-E（Y））2p1+（y2-E（Y））2p2+（y3-E（Y））2p3+（y4-E（Y））2p4
=（x1-c-（E（X）-c））2p1+（x2-c-（E（X）-c））2p2
+（x3-c-（E（X）-c））2p3+（x4-c-（E（X）-c））2p4
=（x1-E（X））2p1+（x2-E（X））2p2+（x3-E（X））2p3+（x4-E（X））2p4
=V（X）
参考になった数0
この解説の修正を提案する
前の問題（問73）へ
令和7年度（2025年度）追・試験 問題一覧
次の問題（問75）へ